Decoupled Weight Decay Regularization

Loshchilov & Hutter, Arxhiv 2017¹¹This paper appeared in ICLR in 2019 as a poster, and now has about 10,000 citations.

If you’ve heard of the AdamW variant of Adam, then this is the paper introducing it.

Summary

This paper is essentially an extended git commit message on a fix for Adam²²See our review of the Adam paper.. The paper points out that “\(L_2\) regularization” and “weight decay” are not the same. The difference is that the former is a part of the overall objective function, and it adds with the Loss function to produce the gradient. The gradient is then scaled by a learning rate \(\gamma\)³³Note that in the Adam paper, learning rate is \(\alpha\). and mixed with various momentum terms before being used in the weight update. “Weight decay” on the other hand, is, or ought to be, decoupled from the Loss function, and is added to the weight update separately from the gradient and momentum terms.

Who cares? Well for one thing, weight decay ought not to be contributing to the momentum. If there’s always something dragging the model towards the origin, then it’s going to acquire an origin-tending component of its momentum, which throws off the determination of both the weight decay and momentum hyperparameters. Moreover, the momentum term is supposed to smooth out variations in the loss landscape, so why add a stationary term to it? You also might not want the learning rate schedule to apply to weight updates. This is one of those “once you hear it it’s obvious” ideas, but nobody seemed to have been complaining about this.

The experiments show several desirable properties:

In the hyperparameter space of learning rate vs. weight decay, there is less interaction between them in AdamW than in regular Adam. (First figure below.)
AdamW has better train-test generalization than other optimizers, including Adam, but still not quite as good as SGD. (Second and third figures below.)
Weight decay has a more salutary effect for AdamW than it does for regular Adam. (Also first figure.)
SGD can also benefit from decoupling weight decay from \(L_2\) regularization. (First and third figures.)

Decoupling weight decay vs. learning rate

To show that weight decay and learning rate are decoupled, meaning that they don’t interact with test error, the paper shows this heatmap comparing weight decoupled versions of Adam and SGD. Warmer colors have higher error. Note that Adam produces higher error, which is something the Adam paper doesn’t mention. Decoupling is where the low-error hyperparameter region is more bowl shaped, where the major axes of the bowl align with the axes of the plot.

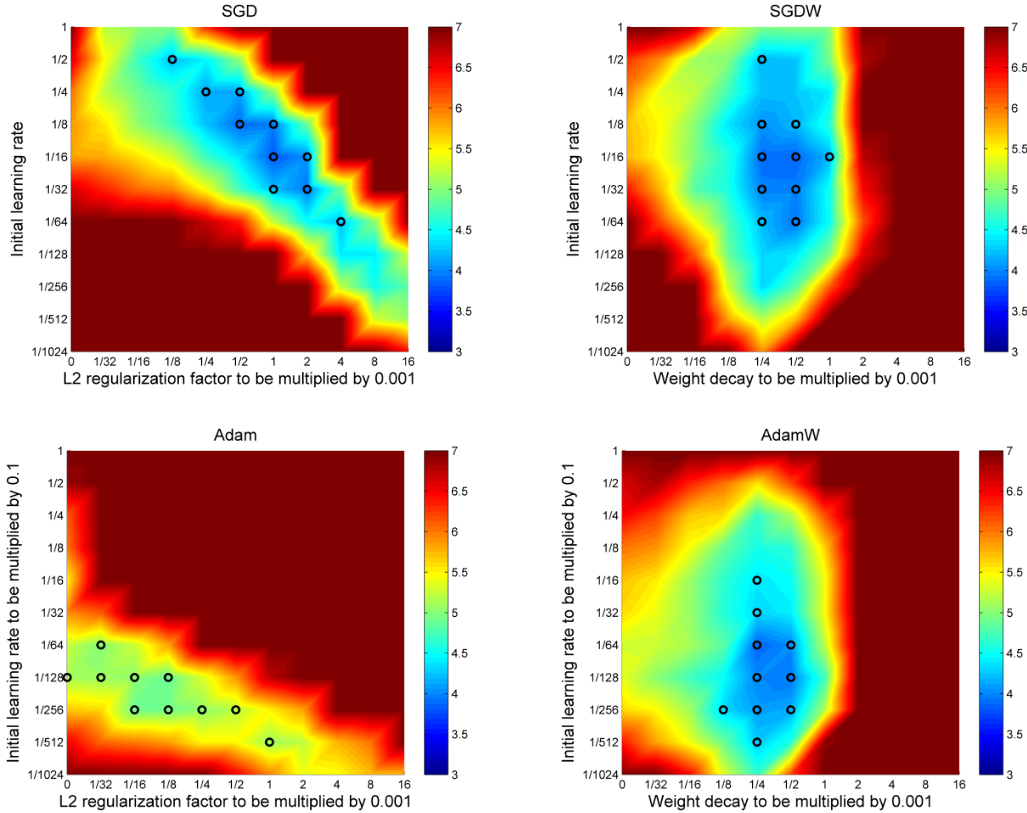
Better generalization

This plot is perhaps most interesting, to me at least, because they drop the time dimension completely. It is simply a scatter plot of train loss vs. test error, and you can see that regular Adam has the characteristic up-turn of an overfit, (i.e., training loss getting lower while test error stays where it is,) while AdamW has less.

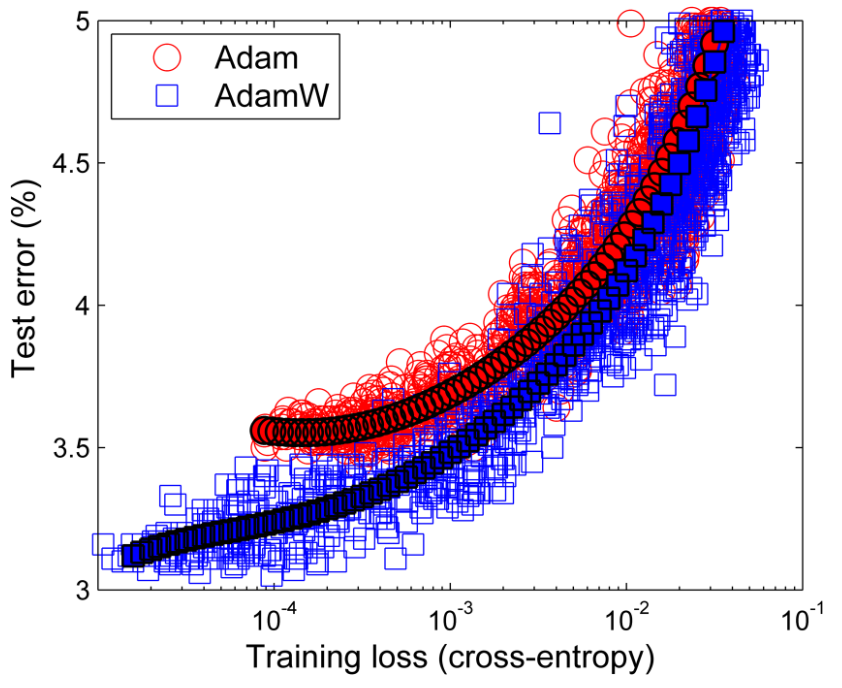
Warm restarts

The paper also describes a “warm restart” trick, which boils down to decreasing the LR on a somewhat more aggressive schedule, and then periodically re-raising it. This is what that looks like – the black and red lines that bounce back and forth are ones where LR decays rapidly and then bounces back up again. In any case, we can see that

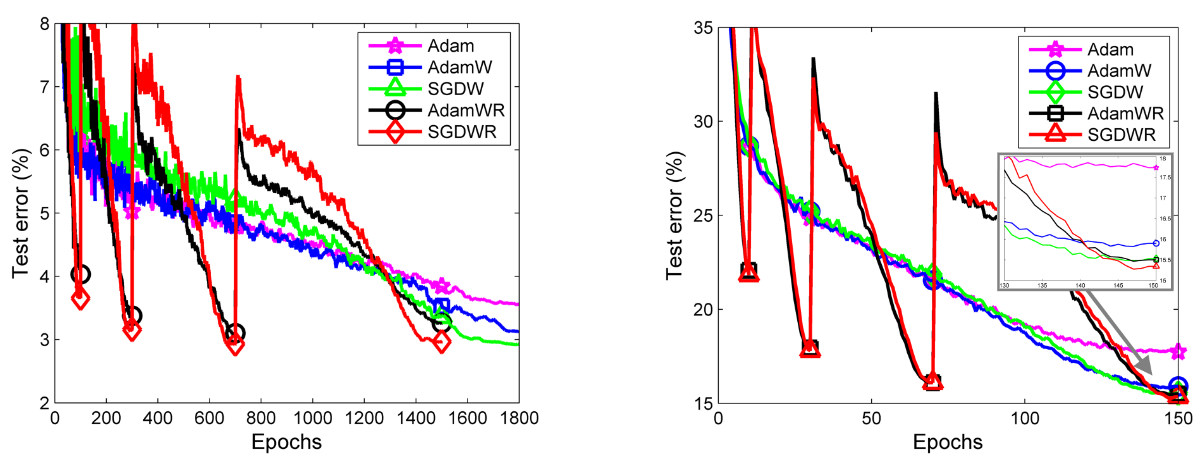
The warm restart methods clearly find much better solutions early on, and their minima lie on a much more quickly decreasing curve, yet, in the end they take almost as many steps to reach minima that are about as good as their non-restarting counterparts.

The paper proposes this effect, i.e., the unintended coupling between weight decay and momentum, as a possible explanation for why Adam often produces less accurate models than standard SGD with weight decay. But on this plot, SGD still seems to eke out a little better.

My observations

There are several notable things about this paper:

The theoretical part is appropriately light, and it feels like in order to fill the space they belabor the main point a bit.
The experiments are interesting, innovative and informative. The paper is very much worth reading for that.
Though it is a 2019 paper, they point out that several works have been using this idea as AdamW going back as far as 2016, and also that it has already been incorporated into pytorch, tensorflow and fast.ai.

I think it’s worth dwelling for a bit on the fact that the well-known high sensitivity of the learning rate, and usefulness of momentum, apply very differently to the loss function than they do to the regularizer, at least in the case of weight decay. In other words, the momentum term only seems to apply to the loss landscape, and not to the interaction of weight decay and loss.

Thanks for reading to the end!

Comments

Comments can be left on twitter, mastodon, as well as below, so have at it.

New post!

Paper outline: The AdamW paper, "Decoupled Weight Decay Regularization"https://t.co/zMcdNqVqjc

Reply here if you have comments.
— The Weary Travelers blog (@wearyTravlrsBlg) August 20, 2023

To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.

Footnotes:

This paper appeared in ICLR in 2019 as a poster, and now has about 10,000 citations.

See our review of the Adam paper.

Note that in the Adam paper, learning rate is \(\alpha\).