Adam: A Method for Stochastic Optimization
Kingma and Ba Arxhiv 2014 1This paper was later published at ICLR in 2015… as a poster. At some point during writing it had exactly 150,000 citations.
Continuing our trend of reviewing foundational works, we now delve into the Adam paper. This paper is from 2014, when Deep
Neural Nets were starting to be featured in mainstream press, but before there were many commercial applications, and
definitely before there were things like MidJourney or ChatGPT. Yet, Adam is still the go-to optimizer for LLMs such as BERT2BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
Devlin et al., Arxhiv 2019, GPT-33Language Models are Few-Shot Learners
Brown et al., NeurIPS 2020
, and therefore probably GPT-44The GPT-4 technical report declines to reveal any training details, citing competitive and safety concerns.
GPT-4 Technical Report
OpenAI, 2023.
Let’s dig in!
Summary
Adam is basically SGD, but with a few extra wrinkles. The name “Adam” is a mnemonic for the fact that the algorithm is adaptive, or more precisely that it adaptively estimates not one, but two moments. In the datasets I’ve monkeyed around with, Adam definitely does converge faster than SGD, but SGD often retains a slight advantage in its final accuracy. The paper also claims that Adam performs a kind of step size annealing, but in practice it still benefits from a learning rate decay.
It’s pretty easy to see why this is the algorithm you would use for training a gigantic model – if the model you’re training is just at the limit of what you can train at all due to its size, then in order to train it in a reasonable amount of time you would need to use the fastest converging algorithm. If you’re a scale maximalist then you don’t need to worry about being perfectly accurate, when you can just wait until someone builds an even bigger GPU cluster and train an even bigger model on it.
The algorithm
We’ve covered the motivation, so now it’s time to dig in to the algorithm itself. Here is the listing from the paper itself:

So what’s happening here? We need a Step size \(\alpha\), two \(\beta\) hyperparameters between \(0\) and \(1\), a function \(f\) to minimize with parameters \(\theta\) and an initial guess \(\theta_0\). Given that you already need \(f\), \(\theta\) and \(\theta_0\) in order to do SGD, we end up with three parameters that we actually care about. Also, in practice, it is very unlikely that you’ll need to tinker with the \(\beta\) hyperparameters, so it really just comes down to this \(\alpha\). Note that they call it a “Step size”, rather than a “Learning rate”, but it functions the same way that a learning rate does in other algorithms. Nevertheless, the paper claims that an advantage of Adam is that the step size really is close to a true step size, or at least it bounds the true step size5It’s important to remember that this “step size” is an element-wise bound on the amount by which any element can change, rather than the magnitude of any whole step..
Next: what state does it keep track of? There are not one, but two momentum vectors, \(m_t\) and \(v_t\), and of course \(t\) is just an iteration counter. The main flow of the algorithm is to,
- Compute a negative cost gradient \(g_t\). This includes all regularizers such as L1 or L2; dropout; and any other gradient noising.
- Update the momentum \(m_t\) by taking a weighed average between \(m_{t-1}\) and \(g_t\). The weight is heavily in favor of the momentum \(m_t\). This is controlled by \(\beta_1\), and given a default value of \(0.9\), it’s pretty heavily weighted towards preserving the momentum, which is the point of momentum.
- Update the squared momentum \(v_t\) by taking a weighted average between \(v_{t-1}\) and squared gradient \(g_t^2\). Once again the weight, controlled by \(\beta_2\) is very heavily weighted towards preserving the momentum, with a default value of 0.999.
- Rescale the two momentum terms by dividing them by \(1 - \beta^t\), where \(\beta\) is the corresponding parameter used above. Note that it is taken as a power of \(t\). At first this means dividing the momentum terms by something small, which will blow them up, but relatively soon the algorithm will be dividing them by something close to \(1\).
- Finally, do the update. As with SGD with momentum, we add the momentum term to \(\theta\), not the gradient, scaled by the step size \(\alpha\). But here is where Adam differs – the update is also divided by the element-wise root of the squared momentum term \(v_t\).
Clearly Adam differs from SGD by keeping track of a squared momentum term. It uses the squared momentum to figure out
what the appropriate step size ought to really be, hence the name. We could think of this as a poor-man’s
Newton’s method.
In Newton’s method, we compute the entire
Hessian matrix of the objective, invert it, multiply the
gradient by it, and then proceed with the update. This is doing something similar, except that it only uses the
diagonal, and a squared gradient rather than the true second derivative6Note that the diagonal of the Hessian is not the same as the squared gradient, however, according to eq. 8 of this
early LeCun paper, this is the “Levenberg-Marquardt approximation”.
Optimal Brain Damage
LeCun et al., NeurIPS 1989
These course notes give a slightly different explanation.. Considering that the inverse of a diagonal matrix is computed
by taking the inverse of the diagonal elements, we could technically consider this as an approximate second order
method.
It’s also worth noting that the division of \(\hat{m_t} / \hat{v_t}\) is done element-wise, meaning that the step is
scaled independently for each element of \(\theta\), which is why the paper claims that it is adaptively scaling the step
size for each element7Compare with the method used in:
Visualizing the Loss Landscape of Neural Nets
Li et al., NeurIPS 2018
See our outline of this paper..
Lastly note the term \(\epsilon\). That’s not a true hyperparameter, since its value should be determined not by the characteristics of \(f\), but by the numeric type of \(\theta\), i.e. \(32\) bit or \(16\) bit float, or whatever. The pytorch version of Adam has a default value of \(10^{-8}\). The keras version uses \(10^{-7}\).
Bias correction
The method devotes a whole step to rescaling \(m_t\) and \(v_t\). The paper explains that this is because it uses \(0\) as an initial guess, and the initial steps of blowing up the two moments are just there to get it away from \(0\), which is a biased initial guess. Almost any initial guess would likely be biased, or at any rate it would contain much less information about the objective function \(f\), so it makes sense to front load the moments heavily with early gradient updates, and smoothly bring them back down to the un-corrected version.
The paper argues that the ratio \(\hat{m_t} / \sqrt{\hat{v_t}}\) is conceptually like a Signal to Noise Ratio (SNR). That is, when there is a large first moment, and not much second moment, estimated over a decaying window, then there is sufficient evidence to take a larger step (relative to the gradient size!) It makes sense that if the recently observed momentum from gradient steps is larger than the root-mean-squared gradient from a much longer history, then a bolder step should be taken. This means it’s doing something like a relaxed – or adaptive – Trust Region method.
The paper then offers another explanation. What we really want is an estimate of the squared gradient \(g_t^2\). However, what we really get is this \(v_t\) thing that is an average over an exponential window: \[ v_t = (1 - \beta_2) \sum_{i=1}^t \beta_2^{t-1} \cdot g_i^2. \] The paper then gives this derivation:
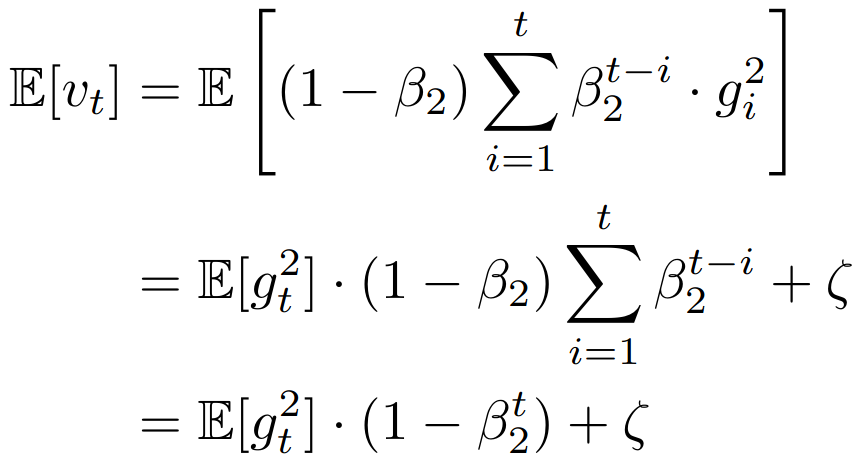
The extra \(\zeta\) term is just an accounting for “non-stationarity” of \(g_t\), i.e., anything that varies as a function of \(t\), apart from the first term. It should just be ignored, because just by using a gradient method with momentum we’re already ignoring it. The last line basically shows that in expectation, \(v_t\) is \((1 - \beta_2^t)\) times \(g_t^2\). Perhaps the simplest way to think of it is that when taking a weighted window average, the coefficients should sum to \(1\)! The last line of this equation is telling us that the coefficients actually sum to \((1 - \beta_2^t)\), so we should divide by that sum to correct for it.
Convergence analysis
An optimization method is no good if it doesn’t ultimately converge, and the paper provides a justification for why it does. The argument goes by borrowing regret-bound machinery from elsewhere. Regret is a concept from online learning where we compare the sum total of the errors of a model that learns from one example at a time against the error of the best model we could have trained if we had had all of the data up front. Here, the idea is to compare the error of all of the \(\theta_t\) iterates against the optimal \(\theta^*\), which can be posed as a regret bound. The appendix has a proof showing that the regret is bounded by \(O(\sqrt T)\).
The main theoretical result makes the following assumptions:
- The function \(f_t\) has bounded gradients: \(\|\nabla f_t(\theta)\|_2 \le G, \|\nabla f_t(\theta)\|_\infty \le G_\infty\). In other words, both the magnitude, and the largest element have a maximum size.
- The distance between successive iterates is bounded: \(\|\theta_n - \theta_m\|_2 \le D, \|\theta_n - \theta_m\|_\infty \le D_\infty\), for any time steps \(m, n\). In other words, there is both a spherical radius that Adam never leaves, and also a largest element-wise divergence between any pair of iterates.
- \(\beta_1^2 < \sqrt{\beta_2}\). This is pretty easy because in practice you usually want \(\beta_1 < \beta_2\). As before, both have to be between \(0\) and \(1\), which means \(\sqrt{\beta_2}\) is actually larger than \(\beta_2\).
- The learning rate \(\alpha\) decreases over time, such that \(\alpha_t = \alpha / \sqrt{t}\).
- \(\beta_1\) also has a decay schedule: \(\beta_{1, t} = \beta_1 \lambda^{t-1}\), for some \(\lambda \in (0, 1)\).
The first is pretty easy to assume, as long as your loss function is reasonably well behaved. The third is true by default, and basically says undefined behaviors are the fault of the operator. The second one is a bit of a crutch. Taken literally, it basically says, “In order to prove that Adam converges, we need to assume that it will never leave some bounded region of \({\mathbb R}^d\).” So what they’re proving is that so long as it doesn’t shoot off to infinity, it will settle down. It should suffice to show that there is a maximum step size that can be taken in any event, but it probably won’t improve the paper to show that, so they just assume it.
The fourth is interesting because in practice one might actually not do that, yet Adam still happily converges. The fifth is… not totally bonkers, but it’s also not common practice, at least not that I’ve ever heard of. Nevertheless, the paper says,
Decaying \(\beta_{1,t}\) towards zero is important in our theoretical analysis and also matches previous empirical findings, e.g. (Sutskever et al., 2013)8On the importance of initialization and momentum in deep learning
Sutskever et al., ICML 2013 suggests reducing the momentum coefficient in the end of training can improve convergence.
The result itself is a monster equation with the regret \(R(T)\) in the LHS, with several \(D^2\), \(D_\infty^2\), and \(G_\infty\) terms on the right. It also features a sum of 2-norms of single gradient elements over time, so if we think of a gradient as a column of a matrix that has \(T\) columns, one for each time step, then the row norms of this matrix play a part in the result. That’s the \(\|g_{i:T,i}\|_2\) term. The paper claims that when there are sparse gradients, this term will be lower, which is why they claim Adam works well on sparse gradients. Of course, this is a bound so how typical is it…?
Here it is in all its gory detail:
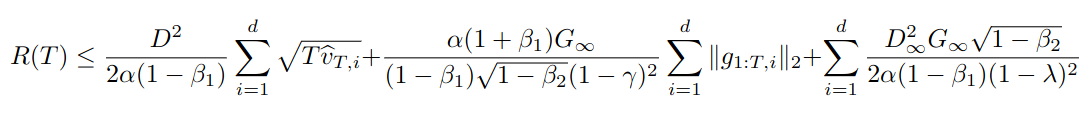
Related works
The paper devotes a whole section to comparing Adam with several existing algorithms, RMSprop and AdaGrad.
RMSProp9Divide the gradient by a running average of its recent magnitude
Tieleman and Hinton; Coursera: Neural networks for machine learning, Lecture 6.5
Yes, that’s how this paper cited RMSProp.
The paper explains it quite nicely.
RMSProp with momentum generates its parameter updates using a momentum on the rescaled gradient, whereas Adam updates are directly estimated using a running average of first and second moment of the gradient. RMSProp also lacks a bias-correction term; this matters most in case of a value of \(\beta_2\) close to \(1\) (required in case of sparse gradients), since in that case not correcting the bias leads to very large stepsizes and often divergence
AdaGrad10Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
Duchi et al., JMLR 2011
The paper gives this update rule for AdaGrad:
\[
\theta_{t+1} = \theta_t - \alpha \cdot g_t / \sqrt{\sum_{i=1}^t g_t^2}.
\]
In other words, there is no window decay, or equivalently \(\beta_1 = 0\) and \(\beta_2 = 1\), and
\(\alpha_t = \alpha\cdot t^{-1/2}\). What’s interesting is that this is equivalent to Adam, specifically with the bias
correction terms. Without them, this would be numerically unstable.
Experiments
The experiments focused on showing that Adam converges faster than other methods. To facilitate comparison, the same random initialization was shared across all methods, and a hyper-parameter grid search was done separately for all methods with the best results being reported for each. The models they examined ranged from tiny, (a simple logistic regression MNIST / IMDB model,) small, (a multilayer perceptron MNIST classifier,) and medium-sized by the standards of the time, (a plain convolutional CIFAR10 classifier).
Logistic Regression
For the logistic regression experiments, they used their learning rate decay schedule, \(\alpha_t = \alpha / \sqrt{t}\). For some reason, RMSProp is examined for the IMDB review task, but the paper doesn’t say why. Otherwise, AdaGrad and SGD with Nesterov momentum are compared. The IMDB task is much sparser, and hence is a good fit for the paper’s claim that Adam does better with sparse features and sparse gradients. Notably, on MNIST, SGD with Nesterov momentum does almost as well as Adam, but on IMDB it fares much worse. AdaGrad does the opposite – well on IMDB, but not as well on MNIST. This also supports the paper’s claim that AdaGrad does well with sparse gradients.
Multi-Layer Perceptron (MLP)
On the MLP experiments they added AdaDelta to the plot, but didn’t mention why. Again, Adam converged faster than the
other methods (in terms of training loss!) The paper also compared Adam with a “Sum of functions” (SFO)11Fast large-scale optimization by unifying stochastic gradient and quasi-Newton methods
Sohl-Dickstein et al., ICML 2014 optimizer, in another set of experiments with dropout disabled, and of course Adam beat it handily. Why another set of
experiments? Because the SOF method has a hard requirement that the cost function must be deterministic, and indeed it
doesn’t converge when dropout is enabled.
Convolutional Neural Net (CNN)
In the CNN experiments the paper dropped RMSProp and AdaDelta, going with just Adam, AdaGrad and SGD / Nesterov, but this time it tried the all with and without dropout. SGD / Nesterov was just about on par with Adam, with or without dropout, and they both left AdaGrad behind. The paper says that in CNNs, the squared momentum term quickly drops to 0, at least compared with the MLP.
Bias Correction
Finally, the paper tests how important this Bias correction term really is. As mentioned, RMSProp is the closest thing there is to Adam but without the bias correction. For this experiment, they trained a Variational Autoencoder. They trained it with several values of \(\beta_1\) and \(\beta_2\), and for each they also tried five values of the learning rate \(\alpha\). The closer \(\beta_2\) is to \(1\), the more bias has to be corrected for. In most cases, RMSProp either aligned perfectly with Adam, or nearly so, or else it blew up spectacularly, especially as \(\beta_2\) went to \(1\), or as \(\alpha\) got larger.
The zinger
The paper has an odd zinger at the end – temporal averaging. That is, the paper makes a last minute proposal, after all
of the experiments are done, to try averaging the weights over several update steps. This can be done uniformly over the
entire training run, or with an exponential decay favoring more recent updates. This trick does work, though as a form
of momentum it has to be used carefully12On the importance of initialization and momentum in deep learning
Sutskever et al. ICML 2013
. I’m aware of at least one successful use case.
So that’s the paper. What did I take away from it?
- It’s interesting that the power of Adam doesn’t just come from merely tracking a squared gradient in addition to a plain momentum, but rather it comes from having the two decay at radically different rates. That is, the second momentum term decays a lot more slowly than the first, and Adam does interesting things when the first moment, with its shorter time horizon, does something different from the second moment, with its much longer time horizon. It makes me wonder what would happen if one simply kept two estimates of the first moment, and just used different decay rates with them. (Since we’re dividing by one, we would probably want to take the absolute value of it…)
- I had one gripe about the experiments – they use different colors for each algorithm across the various plots. That’s a small thing that really makes it annoying to read.
- It’s odd, and yet not odd, that the experiments all examine only training loss not test accuracy. They must have known that their algorithm was producing slightly less accurate classifiers, or else they would have touted that as well. From a certain point of view, however, if an optimizer discovers a lower value of the loss and regularizer combined, then it’s not the optimizer’s fault if test accuracy is less. It is the fault of whoever chose that loss function and regularizer. I’ve seen some papers that did claim, and provide examples, that their optimizer reaches more accurate classifiers, but I tend to agree with this paper – such examples are serendipitous, or should be treated as such.
- SGD with Nesterov is almost as good as Adam in terms of rapid convergence, and given the common wisdom, (which may be only folklore,) that SGD often produces more accurate models, maybe Nesterov is the one you want to use.
Final thoughts
All in all, this is a seemingly minor modification to SGD with momentum, at least from comparing the steps of one with
the other. There are plenty of other cases9Divide the gradient by a running average of its recent magnitude
Tieleman and Hinton; Coursera: Neural networks for machine learning, Lecture 6.5
Yes, that’s how this paper cited RMSProp., 10Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
Duchi et al., JMLR 2011
, 13On the convergence of Adam and Beyond
Reddi et al., ICLR 2018
Decoupled Weight Decay Regularization
Loshchilov and Hutter, ICLR 2019
where small modifications make meaningful improvements. Optimization involves a lot of compounding of effects, which
means that even seemingly small effects can lead to wildly different outcomes. And on such niceties hang the
outcomes of giant experiments.
Thanks for reading to the end!
Comments
Comments can be left on twitter, mastodon, as well as below, so have at it.
New post!
— The Weary Travelers blog (@wearyTravlrsBlg) July 30, 2023
Paper outline: Bayesian Learning via Stochastic Gradient Langevin Dynamicshttps://t.co/9mEIeRLQKD
Reply here if you have comments.
To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.
Footnotes:
This paper was later published at ICLR in 2015… as a poster. At some point during writing it had exactly 150,000 citations.
BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
Devlin et al., Arxhiv 2019
Language Models are Few-Shot Learners
Brown et al., NeurIPS 2020
The GPT-4 technical report declines to reveal any training details, citing competitive and safety concerns.
GPT-4 Technical Report
OpenAI, 2023
It’s important to remember that this “step size” is an element-wise bound on the amount by which any element can change, rather than the magnitude of any whole step.
Note that the diagonal of the Hessian is not the same as the squared gradient, however, according to eq. 8 of this
early LeCun paper, this is the “Levenberg-Marquardt approximation”.
Optimal Brain Damage
LeCun et al., NeurIPS 1989
These course notes give a slightly different explanation.
Compare with the method used in:
Visualizing the Loss Landscape of Neural Nets
Li et al., NeurIPS 2018
See our outline of this paper.
On the importance of initialization and momentum in deep learning
Sutskever et al., ICML 2013
Divide the gradient by a running average of its recent magnitude
Tieleman and Hinton; Coursera: Neural networks for machine learning, Lecture 6.5
Yes, that’s how this paper cited RMSProp.
Adaptive Subgradient Methods for Online Learning and Stochastic Optimization
Duchi et al., JMLR 2011
Fast large-scale optimization by unifying stochastic gradient and quasi-Newton methods
Sohl-Dickstein et al., ICML 2014
On the importance of initialization and momentum in deep learning
Sutskever et al. ICML 2013
On the convergence of Adam and Beyond
Reddi et al., ICLR 2018
Decoupled Weight Decay Regularization
Loshchilov and Hutter, ICLR 2019
