How does Batch Normalization help optimization?
Santurkar, S., Tsipras, D., Ilyas, A. and Madry, A. 2018. How does batch normalization help optimization? Advances in neural information processing systems. 31, (2018).
Conclusion
The effectiveness of batch normalization (BatchNorm)1See previous post for an overview of the technique and the paper that introduced the concept. during training is likely entirely all due to its side-effect of making the optimization landscape smoother.
Additionally, the authors also show that BatchNorm results in a loss landscape where the initialization is better-behaved.2The authors also present theoretical analyses that suggest that BatchNorm leads to better initialization which is consistent with empirical analysis by Im, Tao and Branson.
Limitation and scope
The paper’s focus is on the effect of BatchNorm on training, and not on generalization (though they note that BatchNorm also has the tendency to improve generalization).
Additionally, while the paper does provide strong evidence that batch normalization efficacy has little to do with the purported distributional stability of layer inputs3As was first suggested in Ioffe, S. and Szegedy, C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. International conference on machine learning (2015), 448–456. , the evidence that the efficacy is entirely due to its smoothing effect on the loss landscape is weaker. Specifically, the paper doesn’t rule out confounding factors.
Reasoning structure
The paper makes two arguments:
- The case against Internal Covariate Shift (ICS).
- The case for loss-landscape smoothing explaining BatchNorm’s effectiveness.
For both arguments the paper presents extensive empirical evidence.4Some details necessarily relegated to the supplemental material. For the latter, the paper additionally presents some theoretical bounds.
Synopsis
The case against Internal Covariate Shift
By injecting noise after BatchNorm layers, the authors induce distributional instability, however, BatchNorm’s effectiveness is largely unaffected.5Section 2.1.
We train networks with random noise injected after BatchNorm layers. Specifically, we perturb each activation for each sample in the batch using i.i.d. noise sampled from a non-zero mean and non-unit variance distribution. We emphasize that this noise distribution changes at each time step
…
[T]he performance difference between models with BatchNorm layers, and “noisy” BatchNorm layers is almost non-existent. … Moreover, the “noisy” BatchNorm network has qualitatively less stable distributions than even the standard, non-BatchNorm network, yet it still performs better in terms of training.
The authors observe6Section 2.2. that the effect of BatchNorm is not positively correlated with a reduction in the input-induced change in the optimization landscape of a layer.
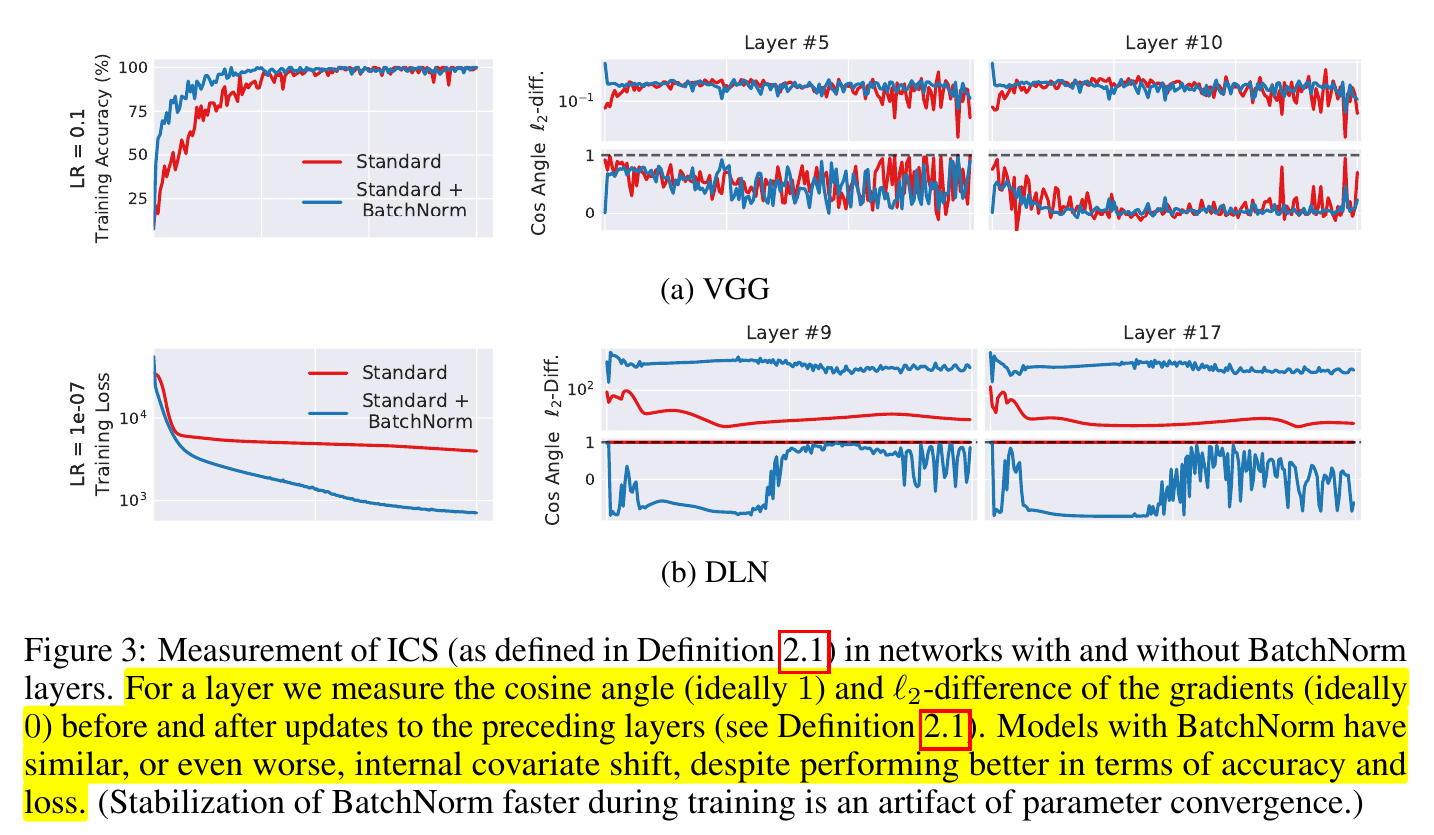
Figure 1: Section 2.2 How does Batch Normalization help optimization?
The case for loss-landscape smoothing
Empirical observations
- BatchNorm reduces the Lipschitz constant of the loss function.7Sections 3.1 and 3.2.
- BatchNorm, additionally, makes the gradients of the loss function more Lipschitz as well.8Sections 3.1 and 3.2., 9As noted in the paper, however, due to “the existence of non-linearities” the Lipschitz constant of the gradient isn’t reduced “in an absolute, global sense.”
- Normalizing by the average of the \(l_p\)-norm before shifting the mean (for \(p = 1, 2, \infty \)) offers comparable performance to BatchNorm without providing distributional stability guarantees.10Section 3.3.
Theoretical analyses11For details, see Section 4 of the paper or Appendix C in the supplemental material
- BatchNorm improves the Lipschitzness of the loss wrt activations. This results in favourable worst-case bounds on the loss landscape wrt layer weights.12Theorem 4.1.
- BatchNorm makes the gradient more predictive by reducing the quadratic form of the loss Hessian with respect to the activations and making it resilient to mini-batch variance.13Theorem 4.4.
- BatchNorm leads to initialization that is closer in \(l^2\)-norm to the set of local optima.14Lemma 4.5.
Comments
Comments can be left on twitter, mastodon, as well as below, so have at it.
New post!
— The Weary Travelers blog (@wearyTravlrsBlg) October 22, 2023
Paper outline: How does Batch Normalization help optimization?https://t.co/yqySFMLwHl
Reply here if you have comments, or use giscus.
To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.
Footnotes:
See previous post for an overview of the technique and the paper that introduced the concept.
The authors also present theoretical analyses that suggest that BatchNorm leads to better initialization which is consistent with empirical analysis by Im, Tao and Branson.
As was first suggested in Ioffe, S. and Szegedy, C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. International conference on machine learning (2015), 448–456.
Some details necessarily relegated to the supplemental material.
Section 2.1.
Section 2.2.
Sections 3.1 and 3.2.
Sections 3.1 and 3.2.
As noted in the paper, however, due to “the existence of non-linearities” the Lipschitz constant of the gradient isn’t reduced “in an absolute, global sense.”
Section 3.3.
For details, see Section 4 of the paper or Appendix C in the supplemental material
Theorem 4.1.
Theorem 4.4.
Lemma 4.5.
