Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Ioffe and Szegedy, ICML 20151As of writing, this paper has just over \(50,000\) citations.
If you’re training neural nets, you’re probably using either Batch Normalization, or Layer Normalization2See our outline of Layer Normalization. Back when this was written, Vanishing and Exploding gradients were still a major problem, and solving it arguably enabled many of the advances we’ve seen since then. Given that Batch size and Learning rate are equivalent, having better control over numerical stability may also let us crank up the batch size even further, allowing even faster training3At least, if you’re training on a whole data-center.. But apart from solving an outstanding issue, Batch Normalization is, like Residual units, an easy drop-in addition to a model that gets an immediate improvement on ImageNet4Architecturally, it’s an easy change, but you have to do other things to take advantage. See the Experiments section., (with that improvement distributed between faster training and better accuracy).
Let’s dig in!
Summary
The paper begins by bringing up an older concept: Covariate Shift5Improving predictive inference under covariate shift by weighting the log-likelihood function
Shimodaira H., J. Statistical Planning and Inference, 2008. That is, when the inputs to a model change, then
the model must change too6As we’ll see, the problem that Batch Normalization tackles isn’t Covariate Shift, it’s actually Univariate Shift.
See also our outline of a paper that rebuts
this notion.. In Deep Neural Nets, all layers but the bottom must deal with Covariate Shift during the course of training. So what?
Well for one thing, if you have a saturating activation function then a sudden shift in the input distribution can put a
unit’s outputs into the saturated region, which can take many gradient steps to get out of. In general, we would expect
that a learned function simply has to depend on the distribution of its inputs.
The paper proposes a simple, partial solution: “Whiten” the univariate distribution of each node’s output. The paper claims that this should provide several benefits:
- Faster training
- Reduced sensitivity to the initial distribution of weights
- Reduced sensitivity to saturating activation functions
- Eliminate or reduce the need for Dropout
In other words, this one trick can give you the same benefits as Adam7Adam: A Method for Stochastic Optimization
Kingma & Ba Arxiv 2014
Technically, Adam will also provide lower objective function values in addition to faster training.,
Glorot initialization8Understanding the difficulty of training deep feedforward neural networks
Glorot & Bengio AISTATS 2010, ReLU9Rectified Linear Units Improve Restricted Boltzmann Machines
Nair, Hinton ICML 2010, and Dropout10Improving neural networks by preventing co-adaptation of feature detectors
Hinton et al. arxiv 2012… just in varying degrees.
Batch Normalization
Whitening a variable is easy, once you know the mean and variance. The trick of this paper isn’t how to whiten a variable11Though, the paper cites several others that tried to collect a lot more than just two statistics per output unit!, the trick is how to estimate means and variances when they’re constantly changing. But hold on – the paper points ou that strict whitening may not be what you want. What you want is constancy over time, so that each unit can learn a function of stable inputs. There’s nothing that says the inputs have to be unit variance.
In other words, there is such a thing as over-normalization, which is where something you do reduces the expressive power of a neural net. The paper motivates it by appealing to the need to learn the Identity function12The Identity function is \(f(x) = x\). The need for being able to express the Identity function was the central motivation of the the ResNet paper.. So, in addition to estimating what the means and variances are, Batch Normalization provides a way to learn what they should be13If you’ve ever used Batch Normalization you’ve probably seen a warning that any layer feeding into a Batch Normalization unit should have its bias disabled… because Batch Normalization is learning its own..
Another way to see why this is necessary is because of the non-linearity of the activation function. The paper points out that for one thing, if the output of each layer is always zero-mean and unit-variance, then the sigmoid activation won’t do very much because most of the inputs will be in the approximately linear part of its domain. That’s the clue – the whole point of non-linearities is that they don’t behave the same everywhere, and if we make everything zero-mean and unit variance, then we’re only exposing them to one locality of that non-linearity. If we let the mean and variance wander, then effectively we’re learning a parameterized non-linearity that acts on fully whitened linear outputs.
So now we know what to do with the means and variances, so how do we estimate them? Easy! Since we’re doing stochastic gradient descent, we get these neat little bootstrap samples, totally for free. So that’s what we do – we compute means and variances within each batch14For the sake of technical completeness, there is one detail – for numerical stability, a small \(\epsilon\) is added to the variance estimate., hence the name. Since the mean and variance interact in a fully algebraic way, there is a simple algebraic way of computing their gradients too, so now we have learnable bias and scale. Tada!
For this to work in Convolutional units, the normalization has to work separately for each location in the kernel, which makes sense because each location is effectively a channels-by-channels linear operator.
Experiments
Earlier on we said that the paper claims the following benefits:
- Faster training
- Reduced sensitivity to the initial distribution of weights
- Reduced sensitivity to saturating activation functions
- Eliminate or reduce the need for Dropout
So does it?
MNIST
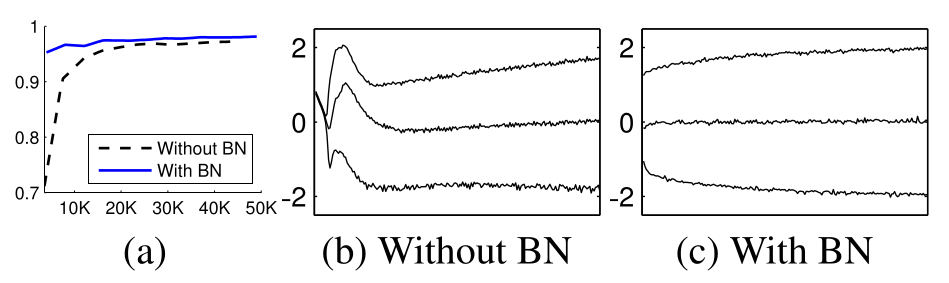
The first thing they looked at is a simple \(3\) -hidden-layer MLP on MNIST, using sigmoid activation. With this experiment they showed two things:
- Higher accuracy, achieved much faster (left panel)
- More stable input distributions at the sigmoid (right panel)
So we have a slam dunk on Faster training, and perhaps reduced sensitivity to the initial distribution of weights.
The Sigmoid function
What about sigmoid saturation? In the margin we have a plot of the sigmoid, from wikipedia. We can see that \(2.0\) really is a good marker for where it saturates, and sure enough, Batch Normalization does a good job of keeping the \(15\) and \(85\) percentiles inside of that range. Still, that means about \(30\%\) of the output units are in the saturating region of the sigmoid. Without Batch Normalization, it hits it early on, but it doesn’t seem to have much problem getting out of the saturating regime either. The paper itself doesn’t say much about saturation here.
ImageNet
So far so good, but this is just MNIST. The paper moves on to the ImageNet task, using a variation of InceptionNet15Going Deeper with Convolutions
Szegedy et al., CVPR 2015, which happens to have been invented by one of the authors. The paper then lists several fine-tuning
adjustments you have to make in order to properly take advantage. So if you’re planning on putting Batch Normalization
to good use, pay careful attention here!
- Increase the learning rate The paper tried \(5\times\) and \(30\times\) the default learning rate.
- Accelerate learning rate decay This is the flip side of increasing the learning rate, so it makes sense.
- Reduce \(\ell_2\) regularization They reduced it by \(5\times\).
- Remove Dropout The paper claims this actually improves validation accuracy, and it will certainly speed up training.
- Shuffle training examples “more thoroughly” Apparently there is an issue with the same examples being in batches together under the sharding they used in distributed training. I wonder if this would help regardless of Batch Normalization, but the paper offers a rationalization that Batch Normalization is a regularizer, and so of course it would better take advantage of the extra randomness.
- Reduce the “photometric distortions” I.e. do less data augmentation. So if Batch Normalization is a regularizer, how come it doesn’t benefit from this extra randomness? The paper says that it helps train “faster” so it’s better to focus more on the “real” images… But then that would help when using say Adam vs SGD too, right? Is this really what’s going on?
- Reduce “Local Response Normalization” This is some kind of Inception feature. Given that Inception was invented by one of the authors of this paper, it’s probably some kind of precursor to Batch Normalization.
If you’re using Batch Normalization in general, the first four are probably the ones you should pay the most attention to. If you believe their reasoning, you might also try dialing back the data augmentation too. To test these, they trained several variants of their model16This was before Adam became the de facto optimizer. The paper doesn’t give training details, but the Inception paper says they used “asynchronous” SGD. Surely Batch Normalization helps with Adam as well, but it makes one wonder how much.:
- Just Inception
- Inception with Batch Normalization (
BN-Baseline) - Inception with Batch Normalization and \(5\times\) the learning rate (
BN-x5) - Inception with Batch Normalization and \(30\times\) the learning rate (
BN-x30) - Inception with Batch Normalization and sigmoid activation instead of ReLU (
BN-x5-Sigmoid)
Results are shown below. The x-axis is in millions of gradient steps.
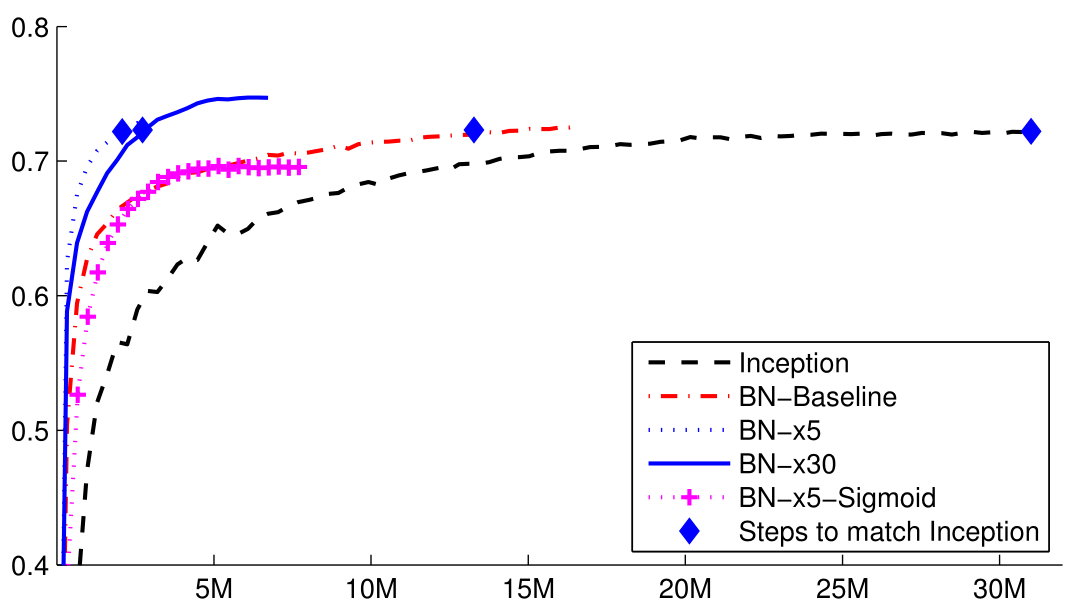
Clearly you can drop in Batch Normalization and get a speedup, but, the clear winner is BN-30x, which means that
there was some benefit to that aggressive training schedule that wasn’t realizable without the numerical stability of
Batch Normalization. It’s interesting that the Sigmoid model is competitive, but still caps out earlier. So maybe Batch
Normalization reduces sensitivity to the saturating regions of the sigmoid, but it doesn’t quite solve the problem all
the way either. It’s at least nice to know that the world isn’t missing out on any major advances on account of not
being able to use the sigmoid.
Here’s the zinger. In order to beat the SOTA on ImageNet, they used an ensemble (fair) and they added Dropout back in, at a lower rate. They also increased the initial weight distribution, which should not have helped if Batch Normalization makes models insensitive to the initial weight distribution…
So in the end I think faster training is a slam dunk, especially if you take advantage of it; you do have reduced need for Dropout, but if you’re squeezing the last bit out of the lemon you still need it; there’s reduced sensitivity to saturating activation functions in case that’s your thing, and reduced (but not eliminated) sensitivity to the initial weights.
So that’s the paper. What did I take away from it?
- Batch Normalization is one of those ideas that once you’ve heard it it’s kind of obvious. It’s not that complicated to motivate, easy to implement, and provides clear benefits. Given that, this is one of the few papers that didn’t really need to be even eight pages to get its idea across… but see the next two points.
- On first reading Section \(2\), it seemed like the paper was making a straw man argument to motivate their approach by first suggesting alternatives that would not work – to either update the weight matrices directly to produce the desired effect, or to update the gradients to produce the desired effect – yet, the paper cites five other papers that do just that. Good ideas really are obvious once you’ve heard them.
- It’s also not obvious until you hear it that plain whitening is not enough. You also need to learn a non-zero mean and a non-unit variance because of how they interact with the non-linearity.
- In a completely different way, this paper uses the original motivation from the ResNet paper – that any unit should be able to learn the Identity function. This is yet another unglamorous good idea that is easy to violate without noticing.
- This paper also hits on another theme that gets my interest – symmetries. A major gap in the current understanding of Deep Neural Nets is a complete characterization of all the equivalent ways to represent the same function17See our outlines of Visualizing the loss landscape and Sharp Minima Can Generalize For Deep Nets for discussion on this.. Batch Normalization is interesting because it induces symmetries in a way that makes it easier for gradient descent to consider novel functions.
Final thoughts
Lately, Large Language Models like GPT-4 and Claude have been demolishing notions of what machine learning can do. It’s hard not to be impressed at their abilities to generalize patterns that few people expected were even present at all in Trillion token-scale internet natural language corpora. Yet, abilities like these were always predicted by machine learning theory, going back to the late 1990s. The limitations were on data, which was ultimately solved by TCP/IP and HTTP/HTML; on compute, which was ultimately solved by NVidia18Or less proximally by TSMC, or even less proximally by ASML., but even then there was still one remaining problem: numerical difficulties. Without a solution to the last one, there is no hope of realizing AI through machine learning, no matter the compute power that can be brought to bear. To me, that makes it the most interesting of the three problems because you simply can’t throw money at the problem.
As we’ve seen in past paper reviews, there is no single solution to numerical difficulties. Rather, results begin to appear when the last bad idea is removed. You can have all the brilliance in the world, and all the resources, but the right wrong idea will still lead you into mediocrity, because sometimes bad ideas look really good. In hindsight, the major advances aren’t necessarily brought about by new ideas19As we saw here, Batch Normalization solves a lot of the same problems as Adam, ReLU, Glorot Initialization and Dropout. As bad ideas are removed, good ideas tend to be rediscovered more frequently because they are all that’s left., but the seemingly insignificant, or moderately significant change that quietly dropped something harmful, leading to a new plateau where everyone will live until the next ground-breaking bad idea is removed.
Thanks for reading to the end!
Comments
Comments can be left on twitter, mastodon, as well as below, so have at it.
New post!
— The Weary Travelers blog (@wearyTravlrsBlg) October 2, 2023
Paper review: The Batch Normalization paperhttps://t.co/kPwFlBppUF
Reply here if you have comments.
To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.
Footnotes:
As of writing, this paper has just over \(50,000\) citations.
See our outline of Layer Normalization
At least, if you’re training on a whole data-center.
Architecturally, it’s an easy change, but you have to do other things to take advantage. See the Experiments section.
Improving predictive inference under covariate shift by weighting the log-likelihood function
Shimodaira H., J. Statistical Planning and Inference, 2008
As we’ll see, the problem that Batch Normalization tackles isn’t Covariate Shift, it’s actually Univariate Shift.
See also our outline of a paper that rebuts
this notion.
Adam: A Method for Stochastic Optimization
Kingma & Ba Arxiv 2014
Technically, Adam will also provide lower objective function values in addition to faster training.
Understanding the difficulty of training deep feedforward neural networks
Glorot & Bengio AISTATS 2010
Rectified Linear Units Improve Restricted Boltzmann Machines
Nair, Hinton ICML 2010
Improving neural networks by preventing co-adaptation of feature detectors
Hinton et al. arxiv 2012
Though, the paper cites several others that tried to collect a lot more than just two statistics per output unit!
The Identity function is \(f(x) = x\). The need for being able to express the Identity function was the central motivation of the the ResNet paper.
If you’ve ever used Batch Normalization you’ve probably seen a warning that any layer feeding into a Batch Normalization unit should have its bias disabled… because Batch Normalization is learning its own.
For the sake of technical completeness, there is one detail – for numerical stability, a small \(\epsilon\) is added to the variance estimate.
Going Deeper with Convolutions
Szegedy et al., CVPR 2015
This was before Adam became the de facto optimizer. The paper doesn’t give training details, but the Inception paper says they used “asynchronous” SGD. Surely Batch Normalization helps with Adam as well, but it makes one wonder how much.
See our outlines of Visualizing the loss landscape and Sharp Minima Can Generalize For Deep Nets for discussion on this.
As we saw here, Batch Normalization solves a lot of the same problems as Adam, ReLU, Glorot Initialization and Dropout. As bad ideas are removed, good ideas tend to be rediscovered more frequently because they are all that’s left.
