Layer Normalization

Ba et al., Arxiv 2016¹¹As of writing, this paper has just over 9000 cites. This is our second paper by Jimmy Lei Ba and also our second by Geoffrey Hinton.

Following our post from last week, this week we’ll be outlining Layer Normalization. Like the AdamW paper, this one is essentially am extended git commit message fixing a popular method. As with AdamW, our interest isn’t in the fix, but in the perspective that made the flaw obvious.

There is support for it in pytorch, and in tensorflow.

Summary

The paper is really a reaction to Batch normalization, and to a lesser extent Weight normalization²²Weight normalization is where you just divide a weight tensor by its 2-norm. As far as I’m aware, there’s no paper for that.. The problem this paper tackles is, as did the Batch Normalization paper, Covariate Shift³³Improving predictive inference under covariate shift by weighting the log-likelihood function
Shimodaira H., J. Statistical Planning and Inference, 2008 That is, if the input distribution changes during learning, then the parameters have to also adjust to the changing inputs in addition to hopefully making progress on the task. Batch normalization uses each minibatch as a bootstrap sample to estimate the mean and variance of each univariate neuron. Batch normalization works well, but has two main drawbacks:

it has an unhealthy dependence on batch size, which can be problematic for small batches, and;
the existence of such a thing as a batch in the first place – at inference time or in online settings there is no equivalent to a batch, and for RNNs[fn::

Recurrent Neural Networks ] you have to do it separately for each time step (for some reason – it just works better). Instead, the paper proposes to estimate the mean and variance parameters separately for each layer, rather than separately for each hidden unit, hence the name. It’s pretty easy to do, and it demonstrably improves over Batch Normalization on most recurrent tasks.

The paper also had this comment that I thought was interesting:

In a standard RNN, there is a tendency for the average magnitude of the summed inputs to the recurrent units to either grow or shrink at every time-step, leading to exploding or vanishing gradients.

i.e. normalization is much more critical for RNNs because they are effectively much deeper than feed-forward nets.

Analysis

The paper does an excellent job of comparing and contrasting the invariances that arise due to Batch, Layer and Weight Normalization.

Here, by “Weight vector” they mean a single column of weight matrix \(W\) that corresponds to a single input into the layer.

In order to understand and interpret the effect of normalization, the paper first notes that the effect of any normalization is to constrain the model parameters to a Riemannian manifold, and, using KL divergence as a metric, the tangent curvature is well approximated by a Fisher information matrix \(F(\theta)\):

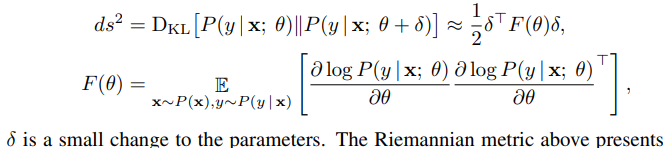
By treating each layer as a bank of GLMs, and a lot of expansion of terms they get to this expression of the Fisher information matrix:

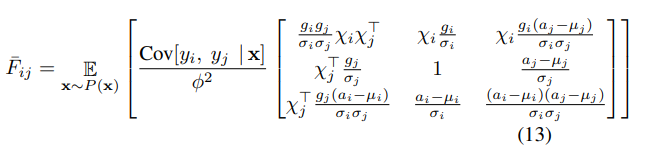
What’s the payoff?

Notice that, comparing to standard GLM, the block \(F_{ij}\) along the weight vector \(w_i\) direction is scaled by the gain parameters and the normalization scalar \(\sigma_i\). If the norm of the weight vector \(w_i\) grows twice as large, even though the model’s output remains the same, the Fisher information matrix will be different. The curvature along the \(w_i\) direction will change by a factor of \(1/2\) because the \(\sigma_i\) will also be twice as large. As a result, for the same parameter update in the normalized model, the norm of the weight vector effectively controls the learning rate for the weight vector.

In other words, each column of \(W\) has its own norm and effectively has its own learning rate. Learning then will proceed until all of the columns have low effective learning rates, which can act as a kind of early stopping criterion.

Experiments

They try Layer Normalization on a variety of recurrent learning tasks and LN consistently and convincingly converges faster than BN, and often gets better accuracy too. This is one of the rare occasions where an experimental section genuinely demonstrates superiority on something⁴⁴But due to selection bias, it’s not rare at all in our coverage…. Tasks investigated include:

Order [co-]embeddings of images and descriptions
Reading comprehension (question answering)
Sentence encoding via “skip-thoughts”
MNIST image drawing
Handwriting sequence generation
Permutation invariant MNIST

Each comes with a code base and a set of metrics, which were markedly improved by adding layer normalization.

They point out an interesting limitation – for convolutional networks, the observed superiority on other tasks largely evaporated. They had this to say about it –

With fully connected layers, all the hidden units in a layer tend to make similar contributions to the final prediction and re-centering and rescaling the summed inputs to a layer works well. However, the assumption of similar contributions is no longer true for convolutional neural networks. The large number of the hidden units whose receptive fields lie near the boundary of the image are rarely turned on and thus have very different statistics from the rest of the hidden units within the same layer

In other words, for convolutional layers, the assumption that all outputs should be identically distributed may not be appropriate.

My Observations

As we saw, the flaw was in the name – Batch Normalization has a dependency on Batch size that doesn’t need to be there. But by taking the transpose of Batch Normalization the paper also subtly changes the meaning of the regularization by making all the weights in each layer pull together.
Layer Normalization makes use of a simple, but often overlooked trick – inducing dependencies between variables by way of regularization. That is, in my grad machine learning course we covered Naive Bayes and Logistic Regression methods as “Linear methods”, meaning that at inference time each variable contributes independently, so in some sense the two have an inductive bias of treating variables in isolation. At my first post-academic job, however, I tried Naieve Bayes on a practical problem, and it was horrible in terms of its Probability Calibration. This is because Logistic Regression does something different – it combines all of the features into one loss, and therefore produces one gradient, so that the trained weight \(w_{i}\) on feature \(i\) reflects its contribution in context of all of the other variables. So what? Well it just so happens that whenever two variables are correlated, they may produce large gradients so they get assigned weights that reflect that tendency. Naive Bayes has no such mechanism, and when you have correlated variables, you will tend to get insanely over-confident predictions. Layer Normalization could be seen as a way of doing some of that combining at each layer, rather than at the loss function, the way Logistic Regression does. That’s really incredible when you consider that the Batch Normalization paper threw up its hands in the face of learning covariances. That’s Quadratic! You might have a singular covariance matrix! Bleh! Well it turns out that there is a way to get some of that for free.
In AlexNet, there was a sliding window approach to normalizing the convolutional channels, and I wonder if it might be beneficial to normalize within layers in a similar sliding window sense. This would mean that different neighborhoods within the layer would be permitted to have different effective learning rates, rather than the extreme case here of single units getting their own learning rates.

Thanks for reading to the end!

Comments

Comments can be left on twitter, mastodon, as well as below, so have at it.

New post!

Paper outline: The Layer Normalization paperhttps://t.co/Z94fBNptEs

Reply here if you have comments.
— The Weary Travelers blog (@wearyTravlrsBlg) October 9, 2023

To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.

Footnotes:

As of writing, this paper has just over 9000 cites. This is our second paper by Jimmy Lei Ba and also our second by Geoffrey Hinton.

Weight normalization is where you just divide a weight tensor by its 2-norm. As far as I’m aware, there’s no paper for that.

Improving predictive inference under covariate shift by weighting the log-likelihood function
Shimodaira H., J. Statistical Planning and Inference, 2008

⁴

But due to selection bias, it’s not rare at all in our coverage…