The paper’s solution is simply to take a max magnitude over all window-averaged squared gradients ever observed, and divide each gradient update by that.

In the regular Adam algorithm, \(\hat{v}_t\) is defined as \(\hat{v}_t = v_t / (1 - \beta_2^t)\)³³Our Adam paper review discusses this in detail.. The term that it divides by is a normalization factor that ensures \(\hat{v}_t\) is an unbiased estimate of the squared gradient. The AMSGrad algorithm dispenses with this, and it also dispenses with the same bias correction for the momentum term – there is no \(\hat{m}_t\) here, while there is one in Adam.

The last step is a bit tricky – the vector \(\hat{v}_t\) is promoted to a diagonal matrix \(\hat{V}_t\), and then it is used as a projection matrix for projecting onto the “feasible set”⁴⁴In some settings e.g., Support Vector Machines there is a feasible set, but for deep neural networks the feasible set is usually the whole of \({\mathbb R}^d\).. If \(x_t - \alpha_tm_t/\sqrt{\hat{v}_t}\) is in the feasible set, then there is no need to pay any attention to the \(\Pi_{\cal F, \sqrt{\hat{v}_t}}()\) part, and we can instead think of the last stem as, \[ x_{t+1} = x_x - \alpha_tm_t / \sqrt{\hat{v_t}}, \] which is the same as in Adam, except for using \(m_t\) instead of \(\hat{m_t}\). At any rate, taking a max over \(\hat{v}\) over the entire training run means that the largest element of \(\hat{v}\) will never decay away, and that’s what the paper means by “long term memory”.

As mentioned above, the paper considers a generalized setting where the average quadratic gradient term \(\hat{v}_t\) expands out to a matrix \(V_t\). The paper immediately restricts \(V_t\) back to being diagonal, because there are very few settings where a non-diagonal \(V_t\) is practical to optimize⁵⁵The paper’s generalized framework also allows for the loss function to be different at each step, though they are almost certainly thinking of the effect of evaluating under different batches, not literally changing the loss function.. The paper’s analysis concludes that convergence requires the difference between successive quadratic terms to be Positive SemiDefinite (PSD), i.e. \(V_{t+1} \succ V_t\). For diagonal matrices, this means they have to be elementwise positive, which is the same as having, \(\hat{v}_{t+1} \ge \hat{v_t}\). In the paper’s generalized framework, the condition can be stated as, \[ \Gamma_{t+1} = \left( \frac{\sqrt{V_{t+1}}}{\alpha_{t+1}} - \frac{\sqrt{V_t}}{\alpha_t} \right). \]

In other words, this means that the step normalization term in the numerator is always growing faster than the learning rate is decreasing in the denominator.

As in Kinga & Ba, the paper proves a couple of complicated learning regret bounds, and in fact they have very similar forms. Compare Theorem 4 from this paper,

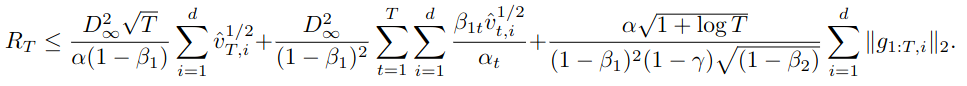
with this regret bound from the Kingma and Ba paper⁶⁶See our Adam paper review for an explanation of the terms such as \(G_\infty\) etc.:

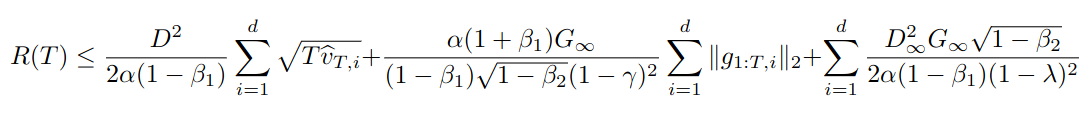
At any rate, the paper claims that it’s bound is considerably better than the \({\cal O}(\sqrt{dT})\) of standard SGD.

The first experiment is a deep dive into the toy problem from the Analysis section, and sure enough AMSGrad destroys Adam. The paper also shows some experiments on CIFAR and MNIST and sure enough it’s a little better than Adam. More specifically, it tends to decrease its loss function even faster than Adam, and in the CIFAR10 plots it looks like it does get to a lower loss value, though it’s a bit hard to tell.