Scaling MLPs: A Tale of Inductive Bias
Gregor Bachmann, Sotiris Anagnostidis, Thomas Hofmann
“Scaling MLPs: A Tale of Inductive Bias”
Arxiv 2023
This is a very new paper – just over a month old at writing – so we can’t do any bibliometrics on it, nor is there any parallax on viewpoints. Nevertheless, it takes its motivation directly from the Attention is all you need paper, making it a nice continuation of the theme. At first blush, “petaFLOP” sounds like something one can only do in a datacenter, until one remembers that there are now 100-terraFLOPs class GPUs, meaning this is a garden variety experiment. Nevertheless, it’s got my attention because it hits very close to the central question – out of all of those FLOPs, what part of them are really essential to learning?
Let’s dig in!
Summary
Multi-Layer Perceptrons (MLPs) are effectively the Turing Machines of Deep Learning. They are easy to analyze and prove things about, but they are not useful as solutions to whole problems1That doesn’t mean they’re not useful as components, as they are an integral part of the Transformer architecture.. Given that, it turns out that almost all of Deep Learning theory is based on properties that are proven about them. This paper points out that there is a serious due diligence gap between theory and practice, and steps in to fill the gap, somewhat.
The paper identifies three key questions that need to be tackled, in the form of a question, a questionable narrative, and a weaker hypothesis:
- Do MLPs reflect the empirical advances exhibited by practical models?
- At large scales of compute, having less inductive bias is beneficial for performance.
- Lack of inductive bias can be compensated by scaling compute.
To study the effect of inductive bias, the paper performs a kind of reverse-ablation study by adding architectural modifications one at a time to a six- or twelve-hidden layer MLP with \(1024\) units per, and then jacking up the compute budget. The paper uses Layer Normalization, but for some reason they add it after the nonlinearity2The Layer Normalization paper says clearly in the abstract: Like batch normalization, we also give each neuron its own adaptive bias and gain which are applied after the normalization but before the non-linearity. (Emphasis mine.). The paper doesn’t say why they do that, and perhaps it’s a recently vogue trick.
The first such modification is ResNet-like inverted bottleneck units, which lift the dimension up before bringing it back down, and adding a skip connection3These are also commonly seen in LLMs nowadays..
For yet another unknown reason, the paper doesn’t say in words what the other modification is, but Table 1 lists “MLP +
DA”, which must be “Data Augmentation”, for which they use flips and random crops, plus something called “MixUp”4mixup: Beyond empirical risk minimization.
Zhang et al., Arxiv 2017
The paper also makes a curious choice of using the brand new LION optimizer5Symbolic discovery of optimization algorithms
Chen et al., Arxiv 2023, for which the Arxiv technical report is itself less than six months old. Perhaps it’s faster? Perhaps they got
another result with Adam? It doesn’t say… that
is, unless you check the appendix where it says they tried AdamW.
The paper says there was a “decrease” in performance. The appendix also says that replacing ReLU with GeLU6Gaussian Error Linear Units
Hendrycks and Gimpel, Arxiv 2016 “boosts results significantly”, but the term doesn’t appear outside of the appendix.
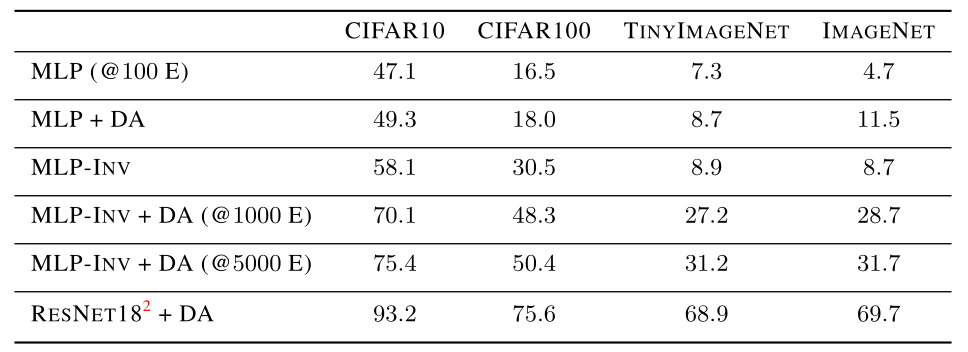
At any rate, to get a baseline, they first train MLPs on several tasks, without any external pretraining. As expected, it’s not great, but that’s never the point with MLPs. Data augmentation helped a smidge, but the inverse bottlenecks helped a lot on both CIFAR tasks. ImageNet went the opposite way. The combination of the two, and also training for \(10\times\) as long, gets a substantial boost, and training for \(50\times\) as long gets a bit more. But, it’s still nowhere near as good as ResNet, and the paper points out that ViT and MLP-Mixers aren’t very good either without massive pre-training on external data. Guess what happens next?
The ’P’ in GPT is for “Pretrained”, and it’s pretty indispensable for Transformers. To take advantage, they pretrained
their MLPs on ImageNet21k, which consists of \(12\) million images and \(11,000\) classes. They ran \(400\) epochs on that
thing, which is quite substantial. They also used the FFCV7FFCV: Accelerating training by removing data bottlenecks
Leclerc et al., CVPR 2023 for loading the data.
To the surprise of (hopefully) no one, this time the results were a lot better. Table 2 shows the results on the widest one with Inverse Bottlenecks. As before, the inverse bottleneck model benefits substantially from Data Augmentation, and at last, the twelve-layer MLP edges out ResNet-18 (without any pre-training, that is,) with the exception of ImageNet, again. The paper makes an astute observation that the Data Augmentation and Inverse Bottlenecks are essential, and the theories don’t seem to obviously imply that. The paper also notes that MLPs, at this scale of pre-training, do better with larger batch sizes. The received wisdom is that Convolutional nets do better with small batch sizes, but see my observation below about that.
Scaling laws
The paper cites three8Beyond human-level accuracy: Computational challenges in deep learning
Hestness et al., POPP 2019
Scaling laws for neural language models
Kaplan et al., 2020
Scaling vision transformers
Zhai et al., CVPR 2022
See also the famous Chinchilla Scaling law paper:
Training Compute-Optimal Large Language Models
Hoffmann et al., Arxiv 2022
recent papers as developing the concept that, given a fixed comptue budget, you can either invest in more parameters
\(P\), or in more data \(D\), and that there is an optimal tradeoff point that can be discovered by fitting a power law
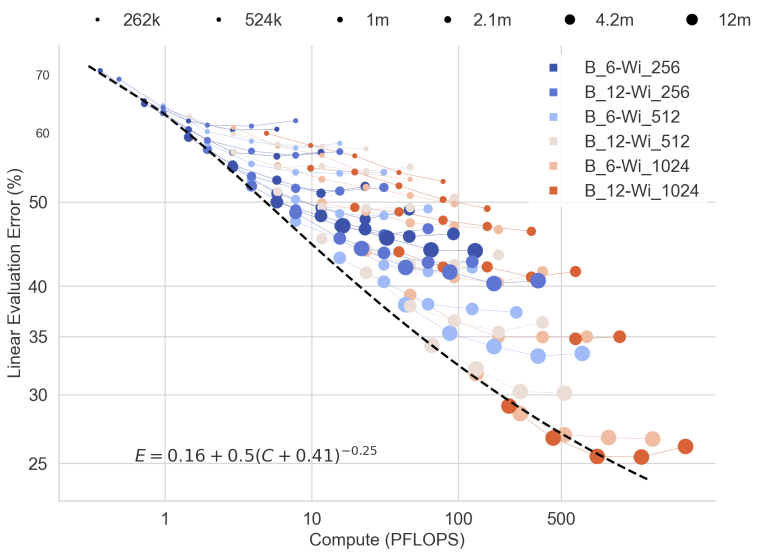
relation between error, FLOP cost per iteration, and the total number of examples seen in training. The figure at the
top of this post shows such relationships in a range of models on the CIFAR100 task, and they paper also has very
similar looking ones for CIFAR10 and ImageNet. Clearly, each setting of architectural parameters finds a different
bottom plateau that seems to follow a predictable pattern. Following the Chinchilla methodology, the fit a power law and
find that for MLPs it favors more passes over the data (\(C^{0.65}\)) rather than more parameters (\(C^{0.35}\)), which does
support the idea that at PFLOP scale, MLPs do have less inductive bias than even transformers (\(C^{0.5}\)).
My observations
- Along the way, the paper gives a rather nice, brief, low-level, self-contained introduction to Convolutions, Vision
Transformers9An image is worth 16x16 words: Transformers for image recognition at scale
Dosovitsky et al., Arxiv 2020 and the MLP-Mixer10MLP-mixer: An all-MLP architecture for vision
Toltsikhin et al., NeurIPS 2021, from a point of view of what relations between variables, (if any,) are encoded by each. The paper makes a particularly careful distinction between using Self-Attention to extract relations between image patch embeddings, vs. the MLP-Mixer way of using transposed Linear operators, one of which globally mixes channels, within each patch, and another that mixes patches in the common embedding space. They even included a helpful diagram. MLP Mixer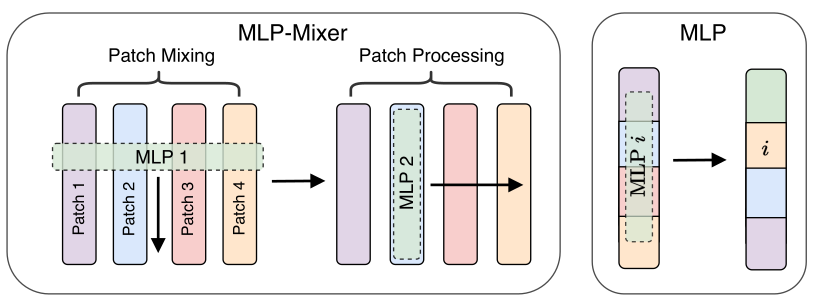
- This paper uses a lot of fancy new methods to study an old problem. If nothing else, it’s a thumb on the pulse of NN training methods.
- I suspect their “large batch sizes are better” result may be less significant than they think. Recalling that learning rate and batch size are fungible, larger batch sizes are equivalent to smaller learning rates, they could have just as well said that they do better with smaller learning rates. On the one hand, maybe at this scale the relation between batch size and learning rate breaks down, or else it’s harder to do a fine-grained parameter search. Either way, any time one examines batch sizes, one should also examine the inverse learning rates as well.
Comments
Comments can be left on twitter, mastodon, as well as below, so have at it.
New post!
— The Weary Travelers blog (@wearyTravlrsBlg) November 12, 2023
Paper outline:
Scaling MLPs: A Tale of Inductive Biashttps://t.co/7ipwQQmnib
Reply here if you have comments, or use giscus.
To view the Giscus comment thread, enable Giscus and GitHub’s JavaScript or navigate to the specific discussion on Github.
Footnotes:
That doesn’t mean they’re not useful as components, as they are an integral part of the Transformer architecture.
The Layer Normalization paper says clearly in the abstract: Like batch normalization, we also give each neuron its own adaptive bias and gain which are applied after the normalization but before the non-linearity. (Emphasis mine.)
These are also commonly seen in LLMs nowadays.
mixup: Beyond empirical risk minimization.
Zhang et al., Arxiv 2017
Symbolic discovery of optimization algorithms
Chen et al., Arxiv 2023
Gaussian Error Linear Units
Hendrycks and Gimpel, Arxiv 2016
FFCV: Accelerating training by removing data bottlenecks
Leclerc et al., CVPR 2023
Beyond human-level accuracy: Computational challenges in deep learning
Hestness et al., POPP 2019
Scaling laws for neural language models
Kaplan et al., 2020
Scaling vision transformers
Zhai et al., CVPR 2022
See also the famous Chinchilla Scaling law paper:
Training Compute-Optimal Large Language Models
Hoffmann et al., Arxiv 2022
An image is worth 16x16 words: Transformers for image recognition at scale
Dosovitsky et al., Arxiv 2020
MLP-mixer: An all-MLP architecture for vision
Toltsikhin et al., NeurIPS 2021